2.2 자기 재료
투자율
(2.1)에서 명시한 대로, 선형 재료에서 //(B//)와 //(H//)는 //( B=\mu H //)로 관련되며, 여기서 //( \mu //)는 재료의 투자율이다. 편의상, 자유 공간의 투자율에 관해서, //( \mu = \mu_0 = 4 \pi \cdot 10^{-7} \mathrm{H/m} //)의 투자율을 표현하는 것이 일반적이다. 그렇게 함으로써, 무차원 상대 투자율(relative permeability)은 다음과 같이 정의된다.
$$ \mu_r = {\mu \over \mu_0} $$ (2.16)
그리고 (2.1)는 //( B = \mu_r \mu_0 H //)로 다시 쓴다. 이러한 관계의 결과, 일반적으로 //( \mu_r \approx 1 //)을 가지는 물질을 비자기재라고 하는 한편, 투자율이 훨씬 큰 물질을 자기재료라고 한다. (2.1) 및 (2.16)에 의해 정의된 허용가능성은 선형, 균질(즉, 균질) 및 동위원소(즉, 모든 방향에서 동일한 성질을 갖는 것) 물질에 엄격하게 적용된다. 그러나 이러한 사실에도 불구하고 (2.1)과 (2.16)은 충분히 넓은 작동 범위에서 충분한 정확도로 보다 복잡한 자기 물질의 실제 성질을 근사하게 나타내기 때문에 광범위하게 사용된다.
강자성 물질(Ferromagnetic materials), 특히 전기강은 모터 구조에 사용되는 가장 일반적인 자기 물질이다. 이들 물질의 투자율은 비선형적이며 다중값을 가져서 정확한 분석이 매우 어렵다. 자계 강도의 비선형 포화 함수인 투자율 외에도, 투자율의 다중값 특성은 재료를 통한 자속 밀도가 주어진 자계 강도에 고유하지 않고, 오히려 자계 강도의 과거 이력 함수라는 것을 의미한다. 이러한 행동 때문에, 강자성 물질의 자기 특성은 흔히 //(B-H//) 곡선, 이력 루프 및 코어 손실 측면에서 그래픽으로 설명된다.
강자성 재료
그림 2-14는 일반적인 강자성 물질의 //(B-H//) 곡선과 몇 개의 이력 루프를 보여주고 있다. 이력 루프는 재료에 서로 다른 진폭의 사인파 편차를 적용하고 //(B//)대 //(H//)를 플롯하여 형성한다. //(B-H//) 곡선은 이력 루프의 끝이나 극단을 서로 연결하여 부드러운 곡선을 형성한다. //(B-H//) 곡선, 즉 DC 자기화 곡선은 투자율의 비선형 특성을 반영하는 평균 재료 특성을 나타내지만 다중값 특성은 무시한다.

//(B-H//) 곡선과 관련된 두 개의 상대 투자율이 있다. 어떤 지점에서 //(B-H//) 곡선의 정규화된 기울기를 상대 미분 투자율이라고 하며 다음과 같이 한다.
$$ \mu_d = {1 \over \mu_o}{dB \over dH} $$ (2.17)
또한 상대 진폭 투자율은 곡선의 한 지점에서 //(B//) 대 //(H//)의 비율이다.
$$ \mu_a = {1 \over \mu_o}{B \over H} $$ (2.18)
이 두 가지 투자율 척도는 재료의 상대 투자율을 기술하는데 유용하다. 상당한 범위의 작동 조건에서는 둘 다 하나보다 훨씬 크다. 그림 2-14에서 알 수 있듯이, 상대적 차분 투자율은 낮은 실장 강도, 중간 실장 강도의 증가 및 피크에 대해서는 작으며, 마지막으로 높은 실장 강도에 대해서는 감소한다. 매우 높은 전계 강도에서, //( \mu_d //)는 1에 접근하고 그 물질은 단단한 포화 상태에 있다고 한다. 일반적인 전기강의 경우, //(1.7 \backsim 2.3 \mathrm{T}//)의 자속 밀도에서 단단한 포화도에 도달하고 //(1.0 \backsim 1.5 \mathrm{T}//)의 부근에서 포화의 시작이 발생한다.
코어 손실
강자성 물질이 다양한 가진으로 가진될 때 에너지는 hysteresis 및 eddy current loss 때문에 소멸된다. 이러한 손실은 실험적으로 분리하기 어렵기 때문에 이들의 결합손실을 보통 측정하여 핵심손실로 부른다. 그림 2-15는 정현파 가진에 대한 일반적인 자재의 코어 손실 밀도 데이터를 보여주고 있다. 이러한 곡선은 재료가 다양한 진폭의 정현파 자기장에 균일하게 노출되었을 때 단위 질량당 손실을 나타낸다. 따라서 재료 블록의 총 코어 손실은 재료의 질량을 그래프에서 판독한 적절한 데이터 값에 곱하여 확인할 수 있다. 브러시리스 영구 자석 모터에서, 모터 강자성 물질의 다른 부분은 다른 자속 밀도 진폭과 다른 파도에 노출된다. 따라서 그림 2-15에 표시된 코어 손실 데이터는 브러시리스 영구 자석 모터에 적용하기가 어렵다. 뒷 장에서는 전동기 코어 손실을 보다 정확하게 예측하기 위해 사인파 코어 손실 데이터를 활용할 수 있는 기술이 개발될 것이다. 그때까지, 코어 손실의 두 가지 요소를 탐구하는 것이 유익하다.

이력 루프가 통과할 때마다 에너지가 손실되기 때문에 이력 손실이 발생한다. 이 손실은 특정 물질의 이력 루프 크기에 정비례하며, 따라서 그림 2-14의 검사로 그 여백의 진폭에 비례한다. 일반적으로 이력 전력 손실은 방정식으로 설명한다.
$$ P_h = k_h f B^n $$
여기서 //( k_h //)는 재료의 종류와 치수에 따라 달라지는 상수로서 //(f//)는 가진 주파수, //(B//)는 재료 내의 자속 밀도 진폭이며, //(n//)은 보통 1.5와 2.5 사이의 재료 의존 지수다.
Eddy current loss는 시간 변화에 따라 강자성 물질 내에서 유도되는 전류에 의해 발생한다. 이러한 유도된 와전류는 재료의 저항으로 인해 재료 소실 전력(즉, //( I^2R //) 손실) 내에서 순환한다. 와전류 전력 손실은 대략 관계에 의해 설명된다.
$$ P_e=k_e h^2 f^2 B^2 $$
여기서 h는 재료의 두께이고 //( k_e //)는 재료에 의존하는 상수다. 이 경우 전력 손실은 자기장 흐름에 수직인 평면의 주파수 제곱, 자속 밀도 진폭 및 재료 두께에 비례한다. 따라서 낮은 주파수에서는 hysteresis 손실이 지배하고 높은 주파수에서는 eddy current loss가 지배할 것으로 예상할 수 있다.
Eddy current loss을 최소화하는 가장 간단한 방법은 재료의 저항성을 높이는 것이다. 이것은 일반적으로 여러 가지 방법으로 행해진다. 첫째, 전기강에는 소량의 실리콘이 함유되어 있다. 실리콘이 있으면 강철의 저항성이 크게 증가하여 eddy current loss이 감소한다. 또, 그림 2-16과 같이 재료의 층화를 이용한 기구를 만드는 것이 일반적이다. 이 얇은 재료들은 얇은 단열재로 코팅되어 있다. 이 층을 함께 쌓으면 스택 방향으로 재료의 저항성이 극적으로 증가한다. 절연재도 비자기성이므로 원하는 플럭스의 흐름에 평행하게 라미네이션 가장자리를 정해야 한다. 위의 방정식으로 기술한 바와 같이, 와전류 손실은 라미네이션 두께의 제곱에 비례한다. 그러므로 높은 주파수에서 더 낮은 손실 작동을 위해서는 얇은 층이 필요하다.

얇은 판으로 된 적층은 주어진 단면적 내에서 자속을 운반할 수 있는 자재의 양을 감소시킨다. 분석에서 이를 보상하기 위해, 적층 인자(stacking factor)는 전체 단면적에 대한 강재 단면적의 비율로 정의된다.
$$ K_{st}={A_{st} \over A_{total}} $$ (2.19)
이 인자는 전체 단면적의 정규화된 양을 나타내며, 적층 자기재의 자속 밀도를 정확하게 계산하는데 중요하다. 대표적인 적층인자는 0.8부터 0.99까지이다.
비록 모터 구조에는 아직 광범위하게 사용되지 않지만, 분말형 강자성 물질은 와전류 손실을 줄이고 3차원 자속 흐름을 허용하기 위해 사용될 수 있다. 이 재료들은 언젠가 선택의 재료가 될 수도 있다. 그것들은 비전도성 수지에 매달려 있는 분말 자성 물질로 구성되어 있다. 사용되는 입자의 작은 크기와 그것들의 전기적인 격리는 재료의 효과적인 저항성을 극적으로 증가시킨다. 단, 이 경우 자재를 통과하는 모든 자속 경로에 비자기 수지가 나타나기 때문에 재료의 효과적인 투자율은 다소 떨어진다.
영구 자석
오늘날에는 많은 종류의 영구 자석 재료를 사용할 수 있다. 이용 가능한 타입으로는 알니코, 페라이트(세라믹), 사마륨-코발트, 네오디뮴-론보론(NdFeB) 등이 있다. 이 중에서, 페라이트 타입은 비싸지 않기 때문에 가장 인기가 있다. 반면 희토류 타입인 사마륨코발트, NdFeB는 최고 성능을 제공한다. NdFeB 자석은 사마륨 코발트보다 훨씬 싸기 때문에 고성능 애플리케이션에서 더 인기가 높다. 대부분의 자석 타입은 접착된 형태와 소결된 형태로 모두 사용할 수 있다. 접착된 자석은 비전도성, 비자기성 수지에 분말 자석 재료를 매달아 형성된다. 이러한 방식으로 형성된 자석은 부피의 상당 부분이 비자기성 물질로 구성되어 있기 때문에 높은 성능을 발휘할 수 없다. 냉장고 문 씰에 있는 자성 물질과 마찬가지로 냉장고 문에 트링킷을 고정하는 데 사용되는 자성 물질이 접합된다. 반면, 성긴 자석은 접합제 없이도 자석이 형성될 수 있기 때문에 고성능이 가능하다. 전체적으로, 각 자석 유형은 브러시리스 영구 자석 모터의 다른 제약조건과 다른 수준의 성능으로 이어지는 다른 특성을 가지고 있다. 이 본문에서는 이러한 자석의 각 유형을 철저히 논하기 보다는 일반적인 특성만을 논한다.
가장 간단한 용어로 표현되는 영구 자석은 큰 히스테리시스 루프를 가진 자석이다. 그러므로 영구 자석을 이해하기 위한 시작점은 그림 2-17에 표시된 첫 번째와 두 번째 사분면인 히스테리시스 루프다. 편의를 위해 자계 강도 축은 //( \mu_o //)에 의해 스케일링되며, 두 축 치수는 테슬라이다. (참고: 이것은 또한 현장 강도 축을 시각적으로 압축한다. 2사분면에 있는 선의 압축되지 않은 경사는 대략 //( \mu_o //)으로 매우 작다.) 그림에 표시된 히스테리시스 루프는 가능한 가장 큰 자계 강도를 측정되지 않은 재료 표본에 적용한 다음 그것을 차단함으로써 형성된다. 이를 통해 재질이 완화되거나, 그림에서 보이는 상단의 곡선을 따라 되돌아갈 수 있으며, 이를 비자화 곡선(demagnetization curve)이라고 한다. 도달한 최종 위치는 자석이 배치된 자기 환경의 기능이다.

그림 2-18a와 같이 무한 투과 재료의 조각에 의해 자석의 양끝이 함께 단락되는 경우, 자석은 보관되어 있다고 하며, 도달한 최종지점은 //(H=0//)이다. 이 지점에서 자석을 떠나는 자속 밀도는 //( B_r //)로 표시된 잔류 자기나 잔존 유도와 동일하다. 잔류 자기는 자석이 스스로 생산할 수 있는 최대 자속 밀도다. 한편, 그림 2-18b와 같이 자석을 둘러싼 투자율이 0이면 자석 밖으로 자속이 흐르지 않고 최종 도달점은 //(B=0//)이다. 이 때, 자석을 가로지르는 자기장 강도의 크기는 //( H_c //)가 영구 자석 사양에 양의 값으로 명시되어 있기 때문에 //( H_c //)로 표현되는 강제력이나 강제력의 마이너스와 동일하다. 0과 무한 사이의 투과도 값의 경우, 작동 지점은 두 번째 사분면, 즉 잔류 자기와 보자력 사이의 어딘가에 있다. 원곡선의 한 지점에서 원점까지 그려진 선의 기울기 크기를 //( P_c //)로 표기한 투과 계수(permeance coefficient)라고 한다. 따라서 //( P_c //)의 관점에서 0과 동일한 투과 계수는 보자력 //(B=0//), //( H=-H_c //)에서 동작하는 것이고, 무한에 해당하는 투과 계수는 잔류 자기 //( B=B_r, \enspace H=0 //)에서 동작하는 것이다.

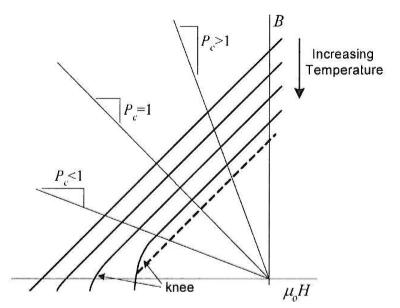
사마륨-코발트 및 NdFeB 재료와 같은 영구 자석 재료는 그림 2-19와 같이 실내 온도에서 두 번째 사분면에 걸쳐 직선 자기화 곡선을 가지고 있다. 일부 페라이트 자석은 상온과 저자속 밀도 값에서 무릎 또는 굴곡이 있다. 2 사분면에 있는 직선 탈자화 곡선의 기울기는 //(\mu_R//)과 동일하며, 여기서//( \mu_R //)은 물질의 상대적인 반동 투자율(relative recoil permeability)이다. 세라믹, 사마륨-코발트, NdFeB 자석의 경우, //( \mu_R //)의 값은 일반적으로 1.0에서 1.2 사이이다. 높은 온도에서 탈자화 곡선은 그림 2-19와 같이 원점을 향해 수축한다. 자기화 곡선이 원점을 향해서 수축함에 따라 자석으로부터 이용 가능한 자속이 떨어져 자석의 성능이 저하된다. 그러나 이러한 성능저하는 온도가 떨어짐에 따라 탈자화 곡선이 이전 상태로 돌아가기 때문에 되돌릴 수 있다. 잔류 자기 //( B_r //)에 미치는 온도의 영향은 대략 선형이며, 따라서 다음과 같이 설명할 수 있다.
$$ B_r(T)=B_r(T_o)[1+\Delta_B(T-T_o)] $$ (2.20)
여기서 //(T//)는 자석 온도, //( T_o //)은 기준 온도, //( B_r(T_o) //)는 //(T_o//)에서 잔류 자기이고, //(\Delta_B//)는 가역 온도 계수다.
온도가 상승함에 따라 원점을 향해 수축하는 것 외에, 사마륨-코발트 및 NdFeB 재료의 자기화 특성에서 무릎은 그림 2-19와 같이 두 번째 사분면으로 이동할 수 있다. 직선으로부터의 이러한 편차는 자속 밀도가 //(-H_c//)에 접근함에 따라 더 빨리 떨어지게 한다. 무릎 부위에서 작동하면 그림 2-19의 점선으로 볼 수 있듯이 자석이 아래의 자화선을 따라 굴절되기 때문에 자화력이 돌이킬 수 없을 정도로 상실될 수 있다. 이렇게 되면 유효 //(B_r//)과 //(H_c//)가 떨어져 자석의 성능이 떨어진다. 이는 바람직하지 않기 때문에 자석이 충분히 큰 투과 계수 //(P_c//)에서 보자력으로부터 벗어나 작동하도록 보장할 필요가 있다.
그림 2-17과 2-19에 나타난 탈자화 곡선은 정상 탈자화 곡선으로 알려져 있다. 이 곡선은 자석이 자기회로에 어떻게 작용하는지 설명하므로 모터 설계에서 유용하다. 이 곡선 외에 자석도 본질적인 탈자화 곡선으로 기술된다. 이 곡선은 환경과 무관한 자석의 고유 자화 특성을 설명한다. 이 곡선은 일반적인 탈자화 곡선과 밀접한 관련이 있지만 일반적으로 모터 설계에는 직접적으로 유용하지 않다.
마지막으로, 이 규격은 일반적으로 자석을 비교하는 데 사용되는 첫 번째 사양이기 때문에, 계속 진행하기 전에 최대 에너지 제품을 정의하는 것이 유익하다. 자석의 최대 에너지 제품 //((BH)_{max}//)는 자석 탈자화 곡선을 따라 자속 밀도와 자계 강도의 최대 제품이다. 이 제품은 에너지 단위를 갖췄다고 해도 실제 저장된 자석에너지가 아니라 자회로에 있는 자석의 성능 능력을 정성적으로 측정한 것이다. 관례상, //((BH)_{max}//)는 보통 수백만 개의 Gauss-Oersteds (MG//(\cdot//)Oe)의 영어 단위에 지정된다. 그러나 일부 자석 제조업체는 입방 미터 당 Joule의 SI 단위를 준수한다 (1MG//(\cdot//)Oe=7.958kJ///(m^3//)). //(\mu_R \approx 1, (BH)_{max}//)가 있는 자석의 경우 통합 투과 계수 작동 지점 근처에서 발생한다. 자기 부피 에너지 밀도 측면에서 //((BH)_{max}//)에서의 작동이 가장 효율적이라는 것을 알 수 있다. 이러한 사실에도 불구하고, 전 항에서 논의한 바와 같이 온도가 상승하면서 돌이킬 수 없는 자기 변형이 가능하기 때문에 모터의 영구 자석은 거의 //((BH)_{max}//)에서 작동되지 않는다.
영구 자석 자기 회로 모델
외부 투과도에 의해 결정된 정적 작동 지점에서 자석의 작동 지점을 이동하려면 외부 자기장을 적용해야 한다. 모터에서 정적 작동 지점은 두 번째 사분면에 위치하며 일반적으로 4이상의 투과 계수에 있다. 모터 권선에 전원이 공급되면 작동 지점은 그림 2-20과 같이 정적 작동 지점을 중심으로 경미한 이력 루프를 따라 동적으로 변화한다. 이 루프는 얇고 기본적으로 자기화 특성과 동일한 기울기를 가지고 있다. 그 결과, 궤적은 다음에서 설명한 직선 자기진단 특성을 근접하게 따른다.
$$ B_m=B_r+ \mu_R \mu_o H_m $$ (2.21)

여기서 //(H_m//)은 음량이다. 왜냐하면 2차 사분면에 있기 때문이다. 이 방정식은 자석이 모든 작동 조건에서 선형 작동 영역에 남아 있다고 가정한다. 자석을 1사분면에 통과시켜 자석을 구동시키는 것은 보통 자화 방향이기 때문에 해를 끼치지 않는다. 단, 외부 자기장이 자석에 의해 개발된 것과 반대하여 조작점을 보자력을 지나 제 3사분면에 진입시킨 경우, 특징의 무릎에 부딪히면 돌이킬 수 없는 자석의 손상을 초래할 수 있다.
(2.21)을 사용해 영구 자석의 자기 회로 모델을 개발할 수 있다. 그림 2-21에 표시된 직사각형 자석을 (2.21)로 설명하도록 한다. 그러면 자석을 떠나는 흐름은
$$ \phi=B_m A_m=B_r A_m+ \mu_R \mu_o A_m H_m $$

여기서 //(A_m//)은 자화 방향으로 향하는 자석의 단면이다. 이 방정식은 (2.4), (2.5), (2.6)을 사용하여 다음과 같이 다시 쓸 수 있다.
$$ \phi=\phi_r + P_m F_m $$ (2.22)
여기서
$$ \phi_r=B_r A_m $$ (2.23)
은 고정 자속 소스이고,
$$ P_m={\mu_R \mu_0 A_m \over l_m} $$ (2.24)
은 자석의 투과성이다. 일반적으로 (2.24)는 자석 누설 투과성이라고 불리지만 여기서 간단히 자석 투과성라고 불리게 된다. 식 (2.22)은 자석의 자기 회로 모델이 그림 2-21과 같이 투과성을 가지는 병렬로 자속 소스임을 암시한다. 이 모델은 물리적 자석이 단면 위로 균일하게 자화되며 선호하는 자기화 방향으로 자화된다고 가정하는 것이 중요하다.
자석 모양이 그림 2-21에 나타낸 직사각형 모양과 다른 경우, 자기 회로 모델을 재평가할 필요가 있다. 방사형 공극을 갖는 브러시리스 영구 자석 모터에서 자석 모양이 그림 2-22와 같이 호로 나타날 수 있다. 이 형태의 자기 회로 모델은 각각 그림 2-21에 주어진 모델을 가지고 있는 미분 길이 자석의 방사형 스택으로 간주하면 찾을 수 있다. 자화 중에 같은 양의 자속이 각각의 미분 길이를 자화한다. 결과적으로, 증가된 면적에 대한 동일한 자속이 더 작은 자속 밀도를 제공하기 때문에, 달성된 잔류 자기는 반지름이 증가함에 따라 선형적으로 감소한다.

그림 2-22에서 호 모양의 자석에 대한 자기 회로 모델을 도출하려면 그림에서 표시한 대로 방사형 두께 //(dr//)의 미분 조각을 고려한다. 이 조각은 미분 자기저항을 가진다.
$$ dR={dl \over \mu A}={dr \over \mu r \theta_m L} $$
여기서 L은 페이지에 있는 자석의 깊이다. 저항과 마찬가지로 자석의 자기저항이 직렬로 추가되기 때문에, 자석의 전체 자기저항은 각 미분 자기저항의 합에 의해 주어진다.
$$ R_m=\int^{r_i+l_m}_{r_i}dR=\int^{r_i+l_m}_{r_i}{1 \over \mu_R \mu_o L \theta_m r}dr={\ln(1+{l_m / r_i}) \over \mu_R \mu_o L \theta_m}$$ (2.25)
이 자기저항의 역수는 그림 2-21에 도시된 바와 같이 자기 투과성 //(P_m//)이다.
$$ P_m=\frac{\mu_R \mu_o L \theta_m}{\ln(1+l_m/r_i)} $$ (2.26)
자화 프로세스 동안 동일한 자속이 각 조각을 통해 흐른다는 사실을 사용하여, 자속 소스는 //(r_i//)에서 표면에 작용하는 잔류 자기에 의해 주어집니다.
$$ \phi_r=B_r A=B_r L \theta_m r_i $$ (2.27)
//( l_m \ll r_i //)인 일반적인 경우에, 자기 투과성 표현 (2.26)을 간단히 하면,
$$ P_m=\frac{\mu_R \mu_o L \theta_m r_i}{l_m} $$ (2.28)
그것은 폭 //(\theta_m r_i//)와 길이 //(l_m//)의 직사각형 블록의 투과성와 같다. 즉, 자석은 //(r_i//)에서 호의 폭에 의해 일정한 폭을 갖는 것으로 보인다.
2.3 예제
이 장에 제시된 개념을 설명하기 위해 그림 2-23에 표시된 자기 장치 및 회로를 고려하십시오. 이 장치는 영구 자석, 고 투과성 강자성 재료 및 공극으로 구성됩니다. 강자성 재료가 매우 높은 투자율을 갖는 것을 고려하면, 자기저항은 무시 될 수 있으며, 그 결과 그림과 같이 자석 등가 회로 및 공극 투과성으로 구성된 자기 회로가 생성된다.

자석을 떠나는 자속은 공극을 가로 지르는 자속과 동일하므로, 즉 //( B_m A_m = B_g Ag //)이므로, 자석과 공극 자속 밀도는
$$ B_g=Bm{A_m \over A_g}=B_mC_{\phi} $$ (2.29)
여기서 //(A_m//)과 //(A_g//)는 각각 자석과 공극의 단면적이며
$$ C_{\phi}={A_m \over A_g} $$ (2.30)
자속 집중 계수(flux concentration factor)입니다. //(C_{\phi}//)가 1보다 큰 경우, 공극에서의 자속 밀도는 자석 표면에서의 자속 밀도보다 크다.
자속 //(\phi//)은 자속 분할 (즉, 전기 회로의 전류 분할에서와 같이)에 의해 쉽게 발견된다.
$$ \phi=\phi_r{P_g \over P_g + P_m} $$
공극이 단순히 //( P_g=\mu_o A_g/g //)로 모델링되면이 방정식을 다시 쓸 수 있습니다.
$$ \phi={\phi_r \over 1+\Big(\mu_R g \Big/ l_m\Big)C_{\phi}} $$ (2.31)
//(\phi//)을 알면 그림에 정의 된대로 회로 전체의 MMF는
$$ F_m={-\phi_r \over P_m P_g}={-B_rA_m \over \mu_R\mu_o \Big({A_m \over l_m}+{A_g \over \mu_Rg}\Big)} $$ (2.32)
이 두 방정식은 자기 회로의 자속 및 MMF 솔루션을 설명합니다. 언급한 바와 같이, 두 방정식은 회로 작동에 대한 중요한 통찰력을 제공하지 않습니다. 방정식에 변수가 너무 많습니다.
그러나, //( B_m=\phi/A_m //) 및 //( H_m=F_m/l_m //)임을 인식하면, 동작점을 정의하는 투과 계수는 다음과 같이 주어진다.
$$ P_c={-B_m \over \mu_oH_m}={l_m \over g}{1 \over C_{\phi}} $$ (2.33)
이 놀랍게도 간단한 결과는 자석 길이 대 공극 길이 및 자속 집중 계수의 비가 투과 계수를 결정한다고 말합니다. 특히 고온에서 자석의 안전한 작동을 위해서는 투과 계수가 1보다 커야하므로 자석 길이는 공극 길이보다 상당히 커야합니다. 또한, 자속 집중, 즉 //(C_{\phi}>1//)을 통해 공극 자속 밀도를 증가시키려는 시도는 투과 계수를 낮춘다.
자속 집중 계수가 증가함에 따라 일정한 투과 계수를 유지하는 데 필요한 것을 고려하면 (2.33)의 기본 중요성을 알 수 있습니다. (2.33)의 분자와 분모에 //(A_mA_g//)를 곱하고 단순화하면
$$ P_c={V_m \over V_g}{1 \over C^2_{\phi}} $$ (2.34)
여기서 //(V_m//)과 //(V_g//)는 각각 자석과 공극 부피입니다. 이제 //(C_{\phi}//)가 //(2C_{\phi}//)로 두 배가되고 공극 부피가 일정하게 유지되면, 일정한 투과 계수를 유지하기 위해 자석 부피가 //(2^2=4//)의 계수만큼 증가해야합니다. 자석 단면적이 일정하게 유지되는 경우, 이는 자석 길이가 4배 증가해야 함을 의미합니다.이 분석의 의미는 영구 자석의 자속을 집중시키는 것은 기하학적으로 증가하는 자석 부피의 단점이 있다는 것입니다.
2.4 요약
이 장에서는 자기 회로 분석의 기본 사항에 대해 설명했습니다. 기본 자기장 개념부터 시작하여 투과성, 자기저항, 자속 및 MMF 개념이 개발되었습니다. 자성 물질 블록, 공극 및 슬롯 형 자성 구조물에 대한 투과 모델이 개발되었습니다. 강자성 및 영구 자석 재료의 특성이 논의되었다. 영구 자석의 자기 회로 모델이 소개되었고 자속 집중의 개념이 설명되었습니다. 이러한 배경을 통해 이제 자기장이 모터의 전기 및 기계 부품과 상호 작용하는 방식에 대해 논의 할 수 있습니다. 이러한 개념은 다음 장에서 설명합니다.
'Book > BLDC Motor' 카테고리의 다른 글
| 브러시리스 영구자석 모터 설계(Ch. 3 전기적 및 기계적 관계: 3.3) (0) | 2019.10.16 |
|---|---|
| 브러시리스 영구자석 모터 설계(Ch. 3 전기적 및 기계적 관계: 3.1~3.2) (0) | 2019.10.15 |
| 브러시리스 영구자석 모터 설계(Ch. 2 자기 모델링: 2.1) (0) | 2019.09.22 |
| 브러시리스 영구자석 모터 설계(Ch. 1 기본 개념: 1.5-1.10) (0) | 2019.09.22 |
| 브러시리스 영구자석 모터 설계(Ch. 1 기본 개념: 1.1-1.4) (0) | 2019.09.22 |




댓글