Chapter 2. Coulomb's Law and Electric Field Intensity Electromagnetic Field

1. 쿨롱의 실험 법칙

    A. 진공 또는 자유공간 내에서 자신의 크기에 비하여 충분히 멀리 떨어져있는 두 개의 작은 물체 사이의 힘은 각각의  물체가 가지고 있는 전하량들에 비례하고 그들 사이의 거리의 제곱에 반비례한다

$$ F=k{Q_1 Q_2 \over R^2} $$

$$ k={1 \over 4 \pi \epsilon_0 } $$

자유공간의 유전율(permittivity)

$$ \epsilon_0=8.854 \times 10^{-12} \doteq {1 \over 36 \pi}10^{-9} \mathrm{F/m} $$

$$ F={Q_1 Q_2 \over 4 \pi \epsilon_0 R^2} $$

    B. //(1//)뉴턴(//( \mathrm{N} //))은 //( 1\mathrm{kg} //)의 질량에 //( 1\mathrm{m/s^2} //)의 가속도를 일으키는데 필요한 힘

    C. 쿨롱은 대단히 큰 전하의 단위이다. 가장 작은 전하량으로 알려져 있는 전자 또는 양자가 갖는 전하량의 크기를 MKS단위인 [//(\mathrm{C}//)]으로 표시하면 //( 1.602 \times 101^{-19} \mathrm{C} //)이며, //( \mathrm{-1C} //)은 약 //( 6 \times 1018 //)개의 전자가 갖는 전하량과 같다. 각각 //( \mathrm{1C} //)의 전하량을 갖는 두 전하가 //( \mathrm{1m} //) 떨어져 있을 때 이들 사이에 작용하는 힘은 //( 9 \times 10^9 \mathrm{N} //)으로 약 //(100//)만톤의 힘과 같다.

 

2. 전계세기(Electric field intensity): 점전하

    A. 임의의 한 전하 //( Q_1 //)을 어떤 위치에 고정시키고, 전하(시험전하, test charge) //( Q_t //)를 //( Q_1 //)주위에서 이동시킬 때, //( Q_t //)는 반드시 힘을 받게 된다. 이것은 전하 //( Q_1 //)에 의해서 어떤 힘의 장(계)(force field)이 존재하고 있음을 나타낸다.

$$ \mathbf{F}_t={Q_1 Q_t \over 4 \pi \epsilon_0 R^2_{1t}} \mathbf{a}_{1t} $$

    B. 전계세기를 단위 양(+)전하량을 갖는 시험전하에 작용하는 벡터힘으로 정의, 전계세기는 //( 1\mathrm{C} //)당 작용하는 힘을 뉴톤/쿨롱(//( \mathrm{N/C} //))으로, 즉 단위전하에 작용하는 힘으로 그 크기를 표시하여야 한다. 전계세기는 볼트/미터(//( \mathrm{V/m} //))라는 실용단위로 표시하고, E를 사용하여 다음과 같이 표현한다.

$$ \mathbf{E}={\mathbf{F}_t \over Q_t} $$

$$ \mathbf{E}={Q \over 4 \pi \epsilon_0 R^2} \mathbf{a}_R $$

 

3. 연속적인 체적전하분포에 의한 전계(Field arising from a continuous volume charge distribution): 체적전하

    A. 실제로는 대단히 작은 입자들이 미소한 간격을 두고 분포되어 있지만, 전하들이 부드럽게 연속적으로 분포되어 있다고 생각하고, 체적전하밀도(volume charge density)로 분포상태를 표시할 수 있다. 이는 물이 원자 크기와 분자 크기의 입자들로 구성되어 있지만 //(1 \mathrm{g/cm^3} //)의 밀도를 가진다고 기술하는 것과 마찬가지이다.

    B. 체적전하밀도는 그리스문자로 //( \rho_v //)로 표시하기로 하며, 그 단위는//( \mathrm{C/m^3} //)이다.

    C. //( \rho_v //)를 사용하면 미소체적 //( \varDelta v//)내에 있는 미소전하량 //( \varDelta Q //)는

$$ \varDelta Q = \rho_v \varDelta v $$

극한 개념을 사용하면

$$ \rho_v = \lim_{\varDelta v \to 0} {\varDelta Q \over \varDelta v} $$

유한체적 내의 총 전하량은 그 체적에 대한 적분

$$ Q= \int_{vol} \rho_v dv $$

 

4. 선전하에 의한 전계(Field of a line charge)

    A. 원통좌표계에서 z축은 //( -\infty //)에서 //( + \infty //)까지 전하가 균일하게 분포되어 있는 균일선전하에 의한 전계는 //( \rho //)에 대해서만 변화한다.

$$ d \mathbf{E}={\rho \over 4 \pi} $$

where

$$ \mathbf{r}= y \mathbf{a}_y = \rho \mathbf{a}_{\rho} $$

$$ \mathbf{r}'=z' \mathbf{a}_z $$

$$ \mathbf{r-r}'= \rho \mathbf{a}_{\rho}-z' \mathbf{a}_z $$

Therefore,

$$ d \mathbf{E}={\rho_L dz'( \rho \mathbf{a}_{\rho}-z' \mathbf{a}_z) \over 4 \pi \epsilon_0 ( \rho^2 + z'^2)^{3/2} } $$

Because only the E_rho component is present, we may simplify

$$ d E_{\rho}={\rho_L \rho dz' \over 4 \pi \epsilon_0(\rho^2 + z'^2)^{3/2} } $$

$$ E_{\rho}= \int^{\infty}_{-\infty} {\rho_L \rho dz' \over 4 \pi \epsilon_0 ( \rho^2 + z'^2)^{3/2} } $$

Integrating by integral tables or change of variale, z'= rho cot theta, we have

$$ E_{\rho}={\rho_L \over 4 \pi \epsilon_0} \rho \Bigg( {1 \over \rho^2}{z' \over \sqrt{\rho^2 + z'^2}} \Bigg)^{\infty}_{-\infty} $$ 

$$ E_{\rho}={\rho_L \over 2 \pi \epsilon_0 \rho} $$

$$ \mathbf{E}={\rho_L \over 2 \pi \epsilon_0 \rho} \mathbf{a}_{\rho} $$

    B. 점전하에 의한 전계세기는 거리의 제곱에 반비례하는 데, 선전하의 경우는 거리에 반비례한다.

    C. 형광등과 같은 광원에서 광원과 가까운 거리에 있는 점에서는 선광원과 같아지며, 멀리 떨어질수록 점광원과 같아진다.

 

5. 면전하에 의한 전계(Field of a sheet of charge)

    A. 대전판을 yz면에 놓고서, 대칭성을 고려하면 전계는 y, z에 대해서 변화할 수 없다. 그 다음에 전계를 구하고자 하는 점에 대해서 대칭적인 위치에 있는 대전판상의 미소전하소들에 의한 전계의 y, z성분들은 서로 상쇄된다. 따라서 //( E_x//)만 존재

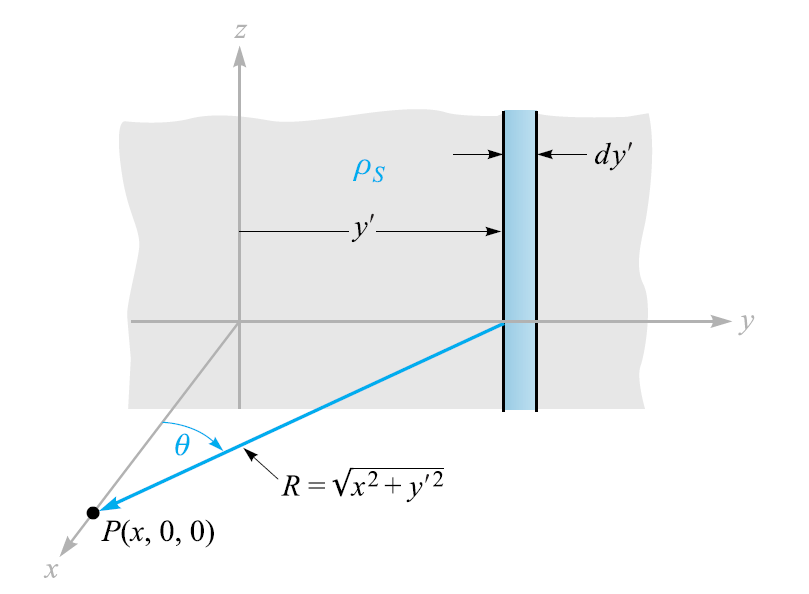
$$ \rho_L = \rho_S dy', \qquad R=\sqrt{x^2 + y^2} $$

The contributon to //(E_x//) at P from this differential-width strip is then

$$ dE_x={\rho_S dy' \over 2 \pi \epsilon_0 \sqrt{x^2+y'^2} } \cos \theta = {\rho_S \over 2 \pi \epsilon_0}{xdy' \over x^2 + y'^2} $$

$$ E_x = {\rho_S \over 2 \pi \epsilon_0} \int^{\infty}_{-\infty} {xdy' \over x^2 + y'^2}={\rho_S \over 2 \pi \epsilon_0} \tan^{-1} {y' \over x} \Bigg]^{\infty}_{-\infty}={\rho_S \over 2 \epsilon_0} $$

$$ E_x=-{\rho_S \over 2 \epsilon_0} $$

$$ \mathbf{E}={\rho_S \over 2 \epsilon_0} \mathbf{a}_N $$

    B. 위에서 전하의 방향은 양전하로부터 밖으로 향하는 방향이 되기 때문이다. 이와 같이 전계의 성분의 부호를 따로 결정하는 번잡성을 피하기 위해서는 판에 직각으로 밖으로 나가는 법선방향을 표시하는 단위벡터 aN을 사용하여 E를 표현.

    C. 이것은 놀라운 답이다. 왜냐하면 이 전계는 그 크기와 방향에서 일정하기 때문이다. 이것이 매우 주목할 만한 결과인 것은, 판으로부터 100만 마일이나 떨어진 점에서도 표면 바로 밖의 점과 꼭 마찬가지로 강하기 때문이다. 다시 빛의 유추로 되돌아가 보면, 매우 큰 방의 천장에 있는 균일한 광원은 마루바닥 위의 조도와 천장 바로 밑의 조도와 동일하다.

    D. 첫 번째 양의 전하밀도 //(\rho_S//), 두 번째 음의 전하밀도 //(-\rho_S, \, \, x=a//) 거리차가 존재

//(x>a//)인 영역

$$ \mathbf{E}_+ ={\rho_S \over 2 \epsilon_0} \mathbf{a}_x \qquad \mathbf{E}_- =-{\rho_S \over 2 \epsilon_0} \mathbf{a}_x \qquad \mathbf{E}=\mathbf{E}_+ + \mathbf{E}_- = 0 $$

//(x<0//)인 영역

$$ \mathbf{E}_+=-{\rho_S \over 2 \epsilon_0} \mathbf{a}_x \qquad \mathbf{E}_-={\rho_S \over 2 \epsilon_0} \mathbf{a}_x \qquad \mathbf{E=E_+ +E_-}=0 $$

//(0<x<a//)일 때

$$ \mathbf{E}_+={\rho_S \over 2 \epsilon_0} \mathbf{a}_x \qquad \mathbf{E}_-={\rho_S \over 2 \epsilon_0} \mathbf{a}_x $$

$$ \mathbf{E=E_+ + E_-}={\rho_S \over \epsilon_0}\mathbf{a}_x $$

E. 이는 실제로 매우 쓸모 있는 결과이다. 예를 들면 판의 넓이가 판 사이의 간격보다 훨씬 큰 공기 커패시터의 평행도체판 사이에서 전계세기는 판의 끝부분에서 충분히 떨어져 있는 점에서는 위의 식과 같이 표시된다. 커패시터 외부의 전계세기는 위의 이상적인 경우와 같이 영이 되지는 않지만 보통 무시한다.

 

6. 전계의 유선과 스케치(Streamlines and sketches of fields)

    A. 유선 스케치

    B. 2차원적인 장에서는 //(E_z=0//)으로 할 수 있으며, 유선, 즉 전력선과 한 전의 전계성분 //(E_x//)및 //(E_y//)들을 표시한 것으로 기하학적으로 다음 관계가 성립

$$ {E_y \over E_x}={dy \over dx} $$

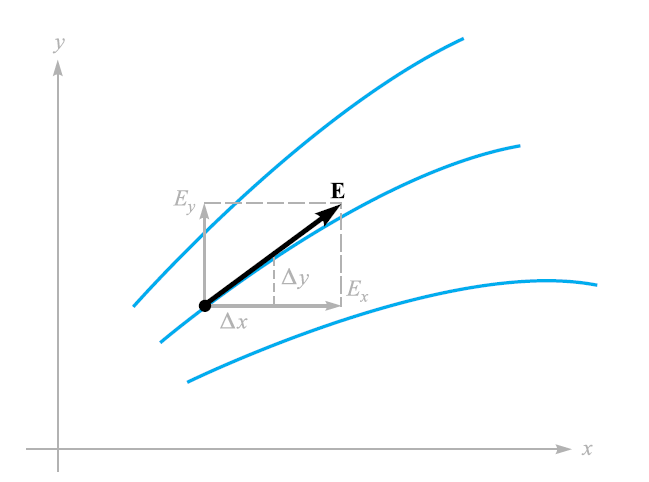
//( E_x//)와 //(E_y//)의 함수적인 관계를 알고 있으면 전력선의 방정식을 구할 수 있다.